Numpy
La structure de base : le array
La contribution majeure de Numpy est de proposer une implémentation performante de tableaux uniformes multi-dimensionnels : le array
[1]:
# on importe le package numpy.
# il est très fréquent d'abréger son nom en 'np'
import numpy as np
[2]:
# Le array est un conteneur qui peut être initialisé
# avec une liste, une liste de listes, une liste de listes de listes, ...
# le niveau d'imbrication décrit le nombre de dimensions du array.
x = np.array([[1, 0.0, 3], [0, 1, 5]])
x
[2]:
array([[1., 0., 3.],
[0., 1., 5.]])
[3]:
# 'ndim' est le nombre de dimensions du array
x.ndim
[3]:
2
[4]:
# 'shape' informe sur la taille de chaque dimension
# Dans l'exemple, x contient 2 listes à 3 éléments.
x.shape
[4]:
(2, 3)
[5]:
# Contrairement aux conteneurs 'classiques', tous les éléments d'un array dovient être du même type.
# Dans l'exemple, des flottants.
x.dtype
[5]:
dtype('float64')
[6]:
# Numpy dispose de types pour gérer des valeurs non-numériques spécifiques : "Not A Number", et "Infinity".
np.NAN, np.Inf
[6]:
(nan, inf)
[7]:
# Ces types peuvent cohabiter avec des valeurs numériques
y = np.array([np.NaN, 2], dtype=float)
print(y.dtype)
y
float64
[7]:
array([nan, 2.])
[8]:
# Des fonctions existent pour créer des array aux remplissages particuliers.
# Un array de 0
np.zeros((2, 3), dtype=int)
[8]:
array([[0, 0, 0],
[0, 0, 0]])
[9]:
# Un array de 1
np.ones(5)
[9]:
array([1., 1., 1., 1., 1.])
[10]:
# Un array avec un contenu non prédéfini, à remplir par la suite
# (le contenu initial du array sera conditionné par ce qu'il y a en mémoire, mais n'épiloguons pas sur le sujet)
np.empty((5,4), dtype=int)
[10]:
array([[-1, -1, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0]])
[11]:
# Au delà des array, numpy dispose de plusieurs fonctions pratiques
# L'équivalent du range() de Python, mais qui retourne un array
np.arange(6)
[11]:
array([0, 1, 2, 3, 4, 5])
[12]:
# Le pendant de np.arange, pour lequel on ne précise pas le pas mais le nombre de valeurs
np.linspace(0,6,5)
[12]:
array([0. , 1.5, 3. , 4.5, 6. ])
[13]:
# Et bien plus encore...
Indexation
L’accès aux éléments d’un array est plus souple que dans le cas des conteneurs de base.
[14]:
# On créer un array d'entiers
x = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(x.dtype)
x
int32
[14]:
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
[15]:
# Le premier indice permet d'accéder aux lignes, ...
x[0]
[15]:
array([1, 2, 3, 4])
[16]:
# ... et le deuxième indice aux colonnes (etc pour les array de dimensions supérieures)
x[0][2] # marche mais peut mieux faire
[16]:
3
[17]:
# ... et le deuxième indice aux colonnes (etc pour les array de dimensions supérieures)
x[0, 2] # voilà, là c'est plus propre
[17]:
3
[18]:
# On peut accéder aux colonnes en utilisant un slice sur le première indice.
x[:, 0]
[18]:
array([1, 5, 9])
[19]:
# Le contenu d'un array peut être modifié
x[0, 0] = -1
x
[19]:
array([[-1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
[20]:
# Il est possible de remplacer plusieurs éléments par la même valeur d'un seul coup.
x[:, 0] = 0
x
[20]:
array([[ 0, 2, 3, 4],
[ 0, 6, 7, 8],
[ 0, 10, 11, 12]])
[21]:
# Toutes les fonctionnalités des slices sont disponibles: arr[start:stop:step]
x[:, ::2]
[21]:
array([[ 0, 3],
[ 0, 7],
[ 0, 11]])
[22]:
# Un accès *très* utile : l'indexation par tableau de booléens
a = np.random.random((5,4))
a
[22]:
array([[0.10193638, 0.31366494, 0.58893349, 0.62615365],
[0.69863562, 0.22738459, 0.85689817, 0.20049676],
[0.73153055, 0.7271929 , 0.74053103, 0.70424826],
[0.07807063, 0.90004515, 0.83373539, 0.57301106],
[0.99646386, 0.19844358, 0.83802383, 0.63492711]])
[23]:
# Admettons : on veut tronquer les valeurs inférieures à 0.5.
# On commence par se créer un "masque"
small = a < 0.5
small
[23]:
array([[ True, True, False, False],
[False, True, False, True],
[False, False, False, False],
[ True, False, False, False],
[False, True, False, False]])
[24]:
# On accède au array par le "masque"...
a[small] = 0
# ... et le tour est joué!
a
[24]:
array([[0. , 0. , 0.58893349, 0.62615365],
[0.69863562, 0. , 0.85689817, 0. ],
[0.73153055, 0.7271929 , 0.74053103, 0.70424826],
[0. , 0.90004515, 0.83373539, 0.57301106],
[0.99646386, 0. , 0.83802383, 0.63492711]])
Arithmétique
Les opérations arithmétiques sur array suivent la convention de l’algèbre linéaire (et sont donc plus intuitive).
[25]:
# Créons un array
x = np.arange(5)
x
[25]:
array([0, 1, 2, 3, 4])
[26]:
# Les opérations entre un array et un nombre sont effectuées sur tous les éléments du array
# Exemple de la multiplication :
# (pour rappel l'opération float * list dans Python duplique la liste)
2.5 * x
[26]:
array([ 0. , 2.5, 5. , 7.5, 10. ])
[27]:
# Les opérations entre array de même taille s'effectuent élément par élément.
y = np.array([10, 11, 12, 13, 14])
[28]:
# Les opérations entre array de même taille s'effectuent élément par élément.
x + y
[28]:
array([10, 12, 14, 16, 18])
[29]:
# Les opérations entre array de même taille s'effectuent élément par élément.
x * y
[29]:
array([ 0, 11, 24, 39, 56])
[30]:
# Numpy dispose de nombreuses fonctions mathématiques : trigo, log, exp, ...
# Les fonctions de Numpy peuvent être appelées sur des array, auquel cas l'opération est appliquée sur tous les éléments.
np.sqrt(y)
[30]:
array([3.16227766, 3.31662479, 3.46410162, 3.60555128, 3.74165739])
Toutes les fonctions disponibles : http://docs.scipy.org/doc/numpy/reference/ufuncs.html#available-ufuncs
[31]:
# Une dernière remarque : numpy peut traiter les opérations arithmétiques entre array de dimensions différentes,
# on parle de "broadcasting".
# Exemple d'application au produit tensoriel :
# On redimensionne x pour avoir un vecteur ligne.
x = x.reshape((1,5))
# On redimensionne y pour avoir un vecteur colonne.
y = y.reshape((5,1))
# Leur produit donne un array de dimensions (5,5).
x*y
[31]:
array([[ 0, 10, 20, 30, 40],
[ 0, 11, 22, 33, 44],
[ 0, 12, 24, 36, 48],
[ 0, 13, 26, 39, 52],
[ 0, 14, 28, 42, 56]])
[32]:
from IPython.display import Image
Image(width=600, url='https://scipy-lectures.github.io/_images/numpy_broadcasting.png')
# source: http://scipy-lectures.github.io
[32]:
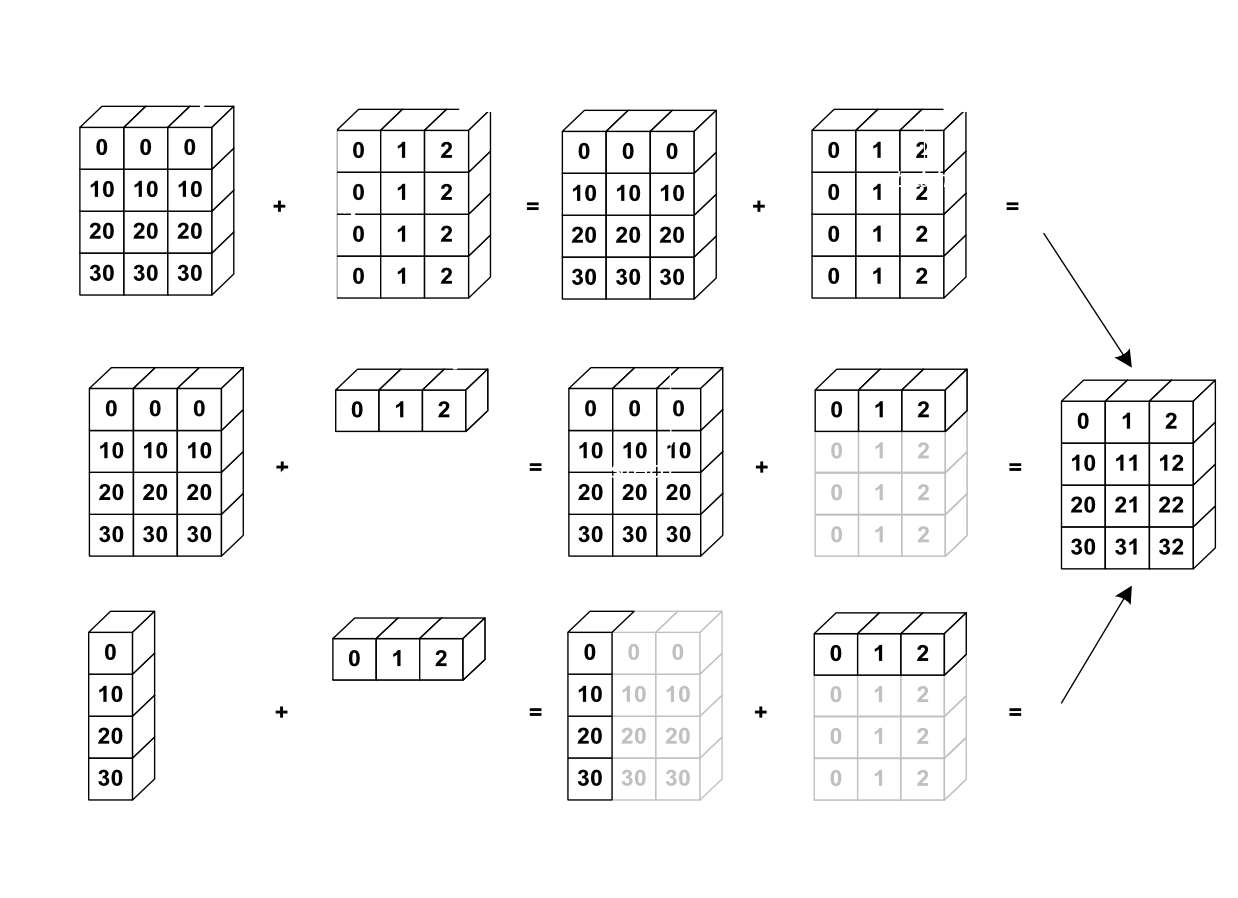
Changer la forme
Il est possible de changer la forme (shape) d’un array sans faire de copie (mais pas toujours)
[33]:
x = np.arange(6)
x
[33]:
array([0, 1, 2, 3, 4, 5])
[34]:
# on peut voir le contenu de x sous la forme d'un array 2d
y = x.reshape((2, 3))
y
[34]:
array([[0, 1, 2],
[3, 4, 5]])
[35]:
# l'information est partagée, pas copiée, on parle de différentes 'views' sur la même donnée.
# modifier le contenu de x a un effet sur y
x[0] = -1
print(x)
print(y)
[-1 1 2 3 4 5]
[[-1 1 2]
[ 3 4 5]]
[36]:
# on peut aussi utiliser l'indexation pour ajouter des dimensions
x[:, np.newaxis]
[36]:
array([[-1],
[ 1],
[ 2],
[ 3],
[ 4],
[ 5]])
[37]:
# ce comportement se combine bien avec le broadcasting
a = np.arange(3)
b = np.arange(5)
a[:, np.newaxis] + b[np.newaxis, :]
[37]:
array([[0, 1, 2, 3, 4],
[1, 2, 3, 4, 5],
[2, 3, 4, 5, 6]])
[38]:
# on peut modifier directement la forme d'un array
x.shape = (3, 2)
x
[38]:
array([[-1, 1],
[ 2, 3],
[ 4, 5]])
Opérations sur les arrays
Quelques fonctions utiles parmi d’autres : np.where(), np.sum(), np.maximum(), np.minimum()
np.where() : « mélanger » deux arrays suivant une condition
[39]:
x = np.arange(10)
x
[39]:
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
[40]:
np.where(x<5, 0, 1)
[40]:
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
np.sum() : sommer un array selon un axe
[41]:
x = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
x
[41]:
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
[42]:
np.sum(x, axis=0)
[42]:
array([15, 18, 21, 24])
[43]:
np.sum(x, axis=1)
[43]:
array([10, 26, 42])
np.maximum(a, b) : construit un array composé du maximum entre a et b (avec du broadcasting)
[44]:
x = np.arange(10)
x
[44]:
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
[45]:
np.maximum(x, 4)
[45]:
array([4, 4, 4, 4, 4, 5, 6, 7, 8, 9])
[46]:
np.minimum(x, 4)
[46]:
array([0, 1, 2, 3, 4, 4, 4, 4, 4, 4])